Thema
kletterblatt
06
8
Person kann mit
einem 5:1 Fakto-
renflaschenzug
durchaus 5 KN erzeu-
gen. Bei 19:1 ist es zwar
nicht knapp das 4fache,
denn es geht Reibungsener-
gie verloren, doch ein normaler
22 KN Karabiner hat in diesem System
nichts mehr verloren.
Eine weitere, interessante Variation des reinen
Potenzflaschenzuges habe ich schon in Abb. 5
dargestellt. Bei diesem Aufbau wird die letzte
lose Rolle jeweils auf das Seil gesetzt, welches
aus der vorherigen Rolle kommt. Der Vorteil
ist hier, dass jede Rolle, mit Ausnahme der ers-
ten, eine lose Rolle ist, also eine „Erleichte-
rung“ darstellt. Außerdem ist der Aufbau ein-
fach, übersichtlich und es bedarf keines zu-
sätzlichen Seiles.
Die Verhältnisse der Mischformen und der, für
die es keinen Namen gibt, sowie aller anderen
Flaschenzüge lassen sich auch berechnen. Die
Methode nennt sich „Freischneiden“. An
einem einfachen Beispiel (Abb. 13) lässt sich
das Prinzip darstellen: man beginnt am Ende
und schreibt an das Seil des Flaschenzuges, an
dem gezogen wird, eine 1. An der ersten Rolle
len bereits ein Verhältnis von 4:1,
drei Rollen ergäben 8:1! Der Vor-
teil dieser Flaschenzüge liegt in
dem geringen Materialaufwand.
Sie sind daher eher in der Berg-
und Höhenrettung zu finden. Aber
auch wir kommen immer wieder in Si-
tuationen, in denen mit wenig viel er-
reicht werden muss.
Bei der Mischung aus beiden und bei Flaschen-
zügen, für die es keine Namen gibt, betreten
wir ein interessantes Feld. Zum einen verlässt
uns unser Physikbuch nun endgültig, zum an-
deren finden wir hier viele Anwendungen für
unsere Arbeit.
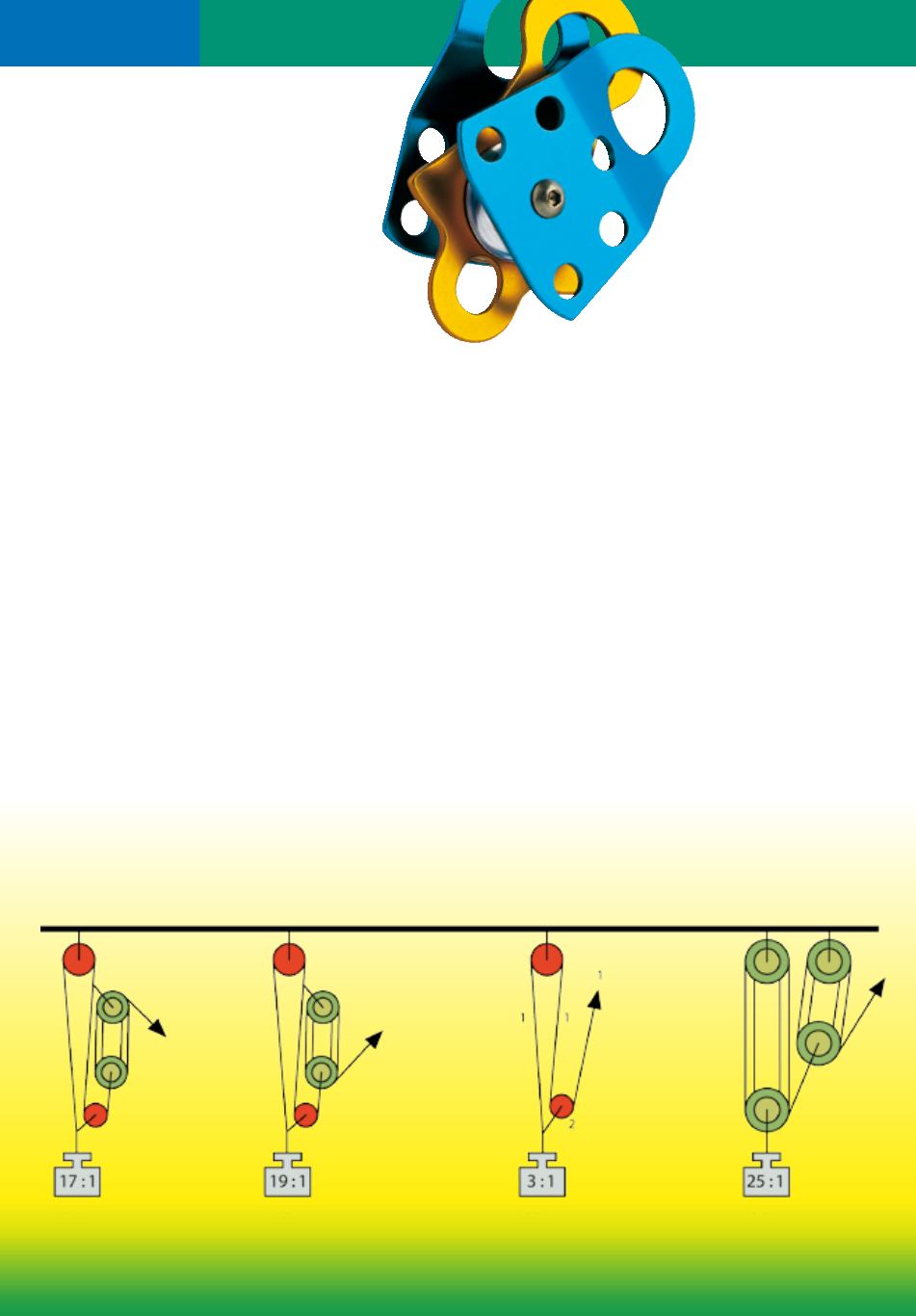
Abb. 10 zeigt einen sehr einfachen Aufbau un-
seres 5:1 Faktorenflaschenzuges, der mit einer
weiteren Rolle kombiniert wurde: schon haben
wir ein Verhältnis von 9:1. Es macht übrigens
in diesem Fall keinen Unterschied, in welche
Richtung gezogen wird. Es ist immer 9:1. Abb.
11 und 12 zeigen die Erweiterung um eine
weitere Rolle: das Verhältnis beträgt nun 17:1
oder 19:1, je nachdem in welche Richtung ge-
zogen wird.
Spätestens hier sollten alle Komponenten auf
ihre Bruchlasten hin überprüft werden. Eine
Abb. 11 Abb. 12 Abb. 13 Abb. 14


