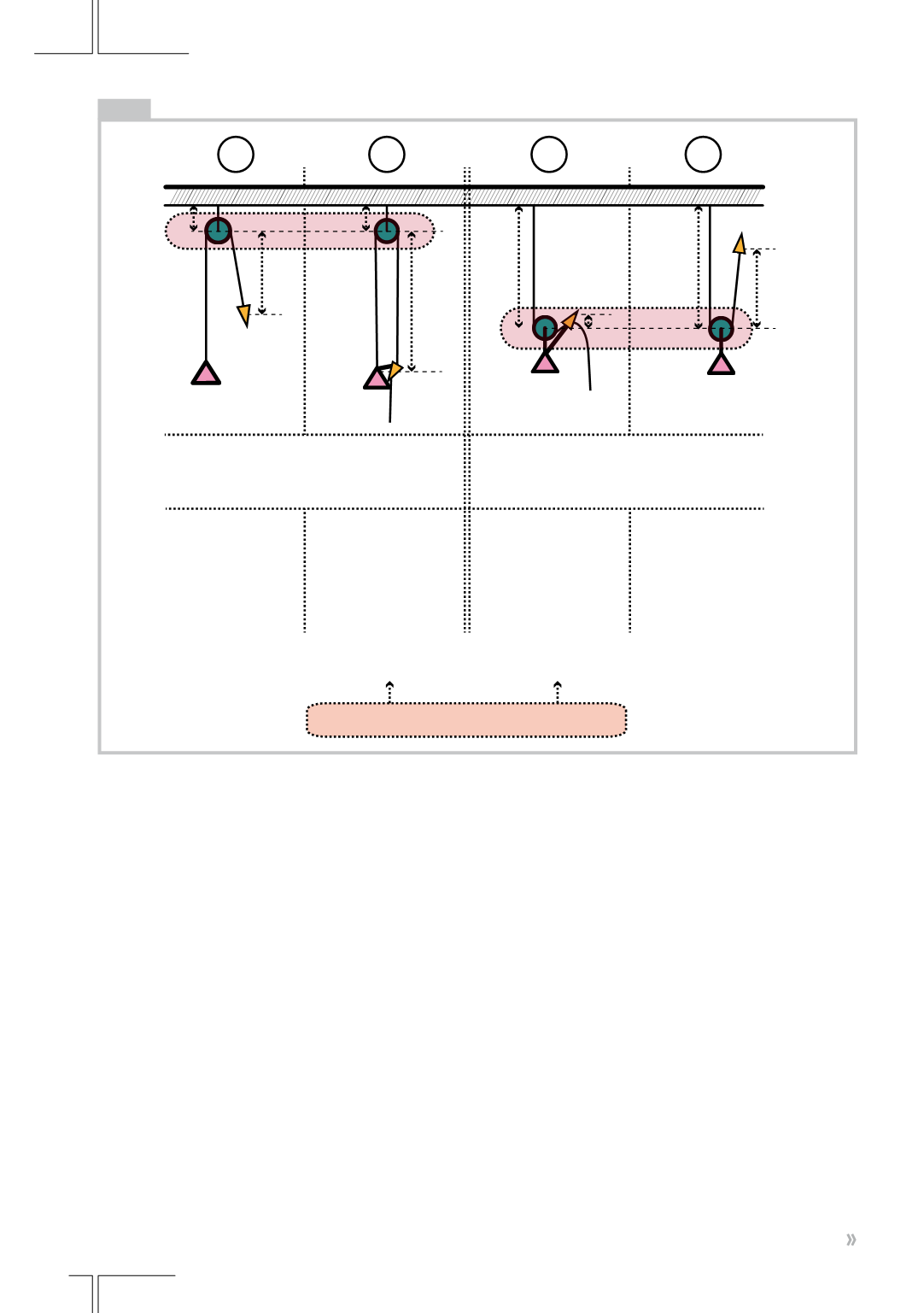
(Grafik 2) Im
Beispiel 1
sehen wir
eine klassische „Feste Rolle“:
Die Last hängt frei, die Umlenkung
befindet sich an einer Struktur, gezo-
genwird vomBoden aus. DieÜberset-
zung imreibungsfreien System ist 1:1,
es ist kein Effekt auf die Übersetzung
vorhanden und damit eine passive
Umlenkung. Das Doppelte der aus
demGewicht der Last resultierenden
Kraft wirkt im Ankerpunkt der Um-
lenkung. Tatsächlich ist diese Rolle
„fest“ imRaum. DerAbstand a vonder
Rolle R zur Decke D ist im ganzen
Hubvorgang gleich. Ebenso bleibt der
Abstand b vom Zugpunkt Z zur Rolle
R in diesem Beispiel immer gleich.
Hier sind wir uns mit der Erklärung
in den Schulbüchern einig.
Wir springen nun zum
Beispiel 4.
Dort erkennen wir die klassische
„Lose Rolle“: Das Seil ist an einer
Struktur angeschlagen, die Last
hängt an einer Umlenkung (zumBei-
spiel in einemSchacht), gezogenwird
wieder vomBoden aus. Die Last wird
stets auf beide Seilstränge verteilt,
daher ergibt sich eine Übersetzung
von 1:2 undwir haben eine aktiveUm-
lenkung. Dem traditionellen Namen
nach ist dieseRolle lose imRaum. Der
Abstand a von der Rolle R zur Struk-
tur D verändert sich im Prozess. Zie-
hen wir am Zugpunkt Z, verändert
sich auch der Abstand vomZugpunkt
Z zur Rolle R. Um die Last die selbe
Distanz wie im Beispiel 1 zu heben,
muss die doppelte Strecke Seil einge-
holt werden. Auch hier sind wir uns
mit der Erklärung in den Schul-
büchern völlig einig.
Das funktioniert so in einfachen Fla-
schenzügen (Faktor- und Potenz-) in
kombinierten sowie in komplexen
Systemen. Doch die Beschreibungen
„lose“ und „fest“ sind relativ, je nach-
dem, von wo das System betrachtet
wird! Wollen wir auch die Klasse der
relativen Flaschenzüge richtig erklä-
ren, zum Beispiel im umlaufenden
System, welches in der SKT verwen-
det wird oder wie sie uns in Aufzügen
begegnen, sind die herkömmlichen
Erklärungsmuster nicht aufschluss-
reich:
ImBeispiel 3
sehenwir den gleichen
Aufbau wie im Beispiel 4: Doch der
Zugpunkt Z ist fest mit der Last ver-
bunden! Weiterhin bewegt sich die
Rolle R imRaum, da sich der Abstand
a von der Rolle R zur Struktur D beim
Ziehen verändert. Allerdings bewegt
sich der Zugpunkt Zmit der Last und
auch mit der Rolle R nach oben. Die
Distanz b von der Rolle R zum Zug-
punkt Zbleibt imProzess gleich. Auch
hebt sich das System exakt um die
eingeholte Länge Seil an. Damit ha-
ben wir ein 1:1 System und eine
1
2
3
4
1:2
1:1
1:2
1:1
a
b
b
R
R
Z
Z
D
Z
Z
a
a
a
Abstand a von der Decke D zur Rolle R
bleibt auch beim Ziehen gleich
>
ruhende Rollen
Abstand b von der
Rolle R zum Zug-
punkt Z bleibt auch
beim Ziehen gleich
>
passiv
„Feste Rolle“
ruhende, lose Rolle ?? bewegte, feste Rolle??
„Lose Rolle“
Abstand b von der
Rolle R zum Zug-
punkt Z verändert
sich beim Ziehen
>
aktiv
Abstand b von der
Rolle R zum Zug-
punkt Z bleibt auch
beim Ziehen gleich
>
passiv
Abstand b von der
Rolle R zum Zug-
punkt Z verändert
sich beim Ziehen
>
aktiv
Abstand a von der Decke D zur Rolle R
verändert sich beim Ziehen
>
bewegte Rollen
b
b
Begri sproblematik
Grafik 2
kletterblatt 2015
10
Flaschenzug
Technik


